Honer’s Volume Equations

 

Honer’s (1967) total volume equation has been widely used throughout eastern North America.  In a study conducted in 1998 (Shailer, et al. 1998) in New Brunswick, Honer’s volume equations were shown to best predict total volume from a set of almost 20 different published volume equations for nine important commercial species.

 

The original form of Honer’s total volume equation (Honer 1967) was:

 

 

where,

 

VTot = Total volume in ft3

D = diameter outside bark (inches) measured at breast height (4.5 ft)

H = total height (ft)

b0 and b1 are species specific regression coefficients.

 

Honer’s equations, as originally developed, were based on the English measurement system.  To make these equations appropriate for the metric system, Honer et al. (1983) developed a series of modifications to convert the cubic–foot volume based on English measurements to cubic–meter volume based on metric measurements.

 

The conversion process was as follows:

 

1. cubic feet to cubic meters conversion:

 

 

where

 

VTot(E) = the total volume in ft3 as estimated from Honer’s original equation (see above) based on D4.5,int (diameter measured in inches at 4.5 ft) and Hft (height measured in feet).

 

2. height in feet to height in meters:

 

Since total height is measured identically in the English system and metric system, the conversion for height is straight forward:

 

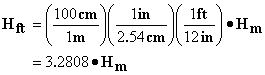
and

 

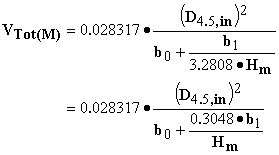
3. dbh in cm (d1.3,cm) to dbh in inches (D4.5,in):

 

The diameter conversion is trickier since the measurement point differs in the two systems.  DBH in the English system is measured at 4.5 ft (1.37 m), while dbh in the metric system is measured at 1.3 m.  The conversion factor has to account for both the conversion from cm to inches as well as the taper in the tree stem (diameter at 1.3 is going to be larger than the diameter at 1.37 m).  To address this issue, Honer et al. (1983) proposed a simple taper function:

 

where,

 

D1.37 = diameter at 1.37 m (4.5 ft) in centimeters

d1.3 = diameter at 1.3 m in centimeters (metric dbh)

c1 = species specific taper coefficient

 

Finally, D4.5,in can be obtained using:

 

 

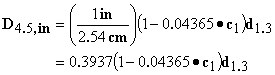
and the volume equation becomes:

 

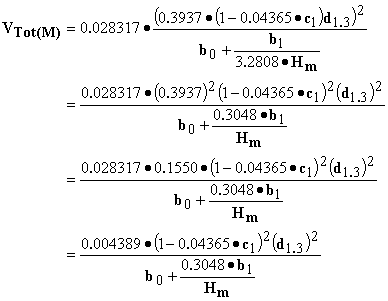
So now we have an estimate of total volume in m3 based on dbh in cm measured at 1.3 m and total height in m that is compatible with the original English total volume estimates in ft3.  This compatibility was crucial since Honer’s (1967) English volume equations were so widely applied and we needed compatible estimates of volume as Canada transitioned from the English system to the metric system; however, as formulated above, we are left with a very messy equation.  To simplify this equation, I propose the following substitutions:

 

and

and

 

The volume equation then becomes:

 

 

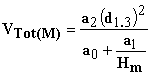
Table 1 gives the original coefficients for Honer’s (1967) volume equation (b0 and b1), the taper coefficient (c1) and the metric derived coefficients (a0, a1, and a2) for the major species found in New Brunswick.

 

Table 1.  Original coefficients for estimating total volume (ft3) based on Honer’s (1967) volume equation, the taper coefficient for conversion of dbh1.3 to DBH1.37 (Honer et al. 1983), and the metric derived coefficents for estimating total volume (m3) by species.

 

Species

Honer's (1967) coefficients

 

Taper

 

   metric derived coefficients

 

b1

b2

 

Coefficient

 

a0

a1

a2

White Pine

0.691

363.676

 

0.184

 

0.691

110.848

0.004319

Red Pine

0.710

355.623

 

0.151

 

0.710

108.394

0.004331

Jack Pine

0.897

348.530

 

0.151

 

0.897

106.232

0.004331

Black Spruce

1.588

333.364

 

0.164

 

1.588

101.609

0.004327

Red Spruce

1.226

315.832

 

0.169

 

1.226

96.266

0.004325

White Spruce

1.440

342.175

 

0.176

 

1.440

104.295

0.004322

Balsam Fir

2.139

301.634

 

0.152

 

2.139

91.938

0.004331

Cedar

4.167

244.906

 

0.155

 

4.167

74.647

0.004330

Hemlock

1.112

350.092

 

0.155

 

1.112

106.708

0.004330

Trembling Aspen

-0.312

436.683

 

0.127

 

-0.312

133.101

0.004341

Balsam Poplar

0.420

394.644

 

0.127

 

0.420

120.287

0.004341

White Birch

2.222

300.373

 

0.176

 

2.222

91.554

0.004322

Yellow Birch

1.449

344.754

 

0.181

 

1.449

105.081

0.004320

Maple

1.046

383.972

 

0.145

 

1.046

117.035

0.004334

Basswood

0.948

401.456

 

0.145

 

0.948

122.364

0.004334

Beech

0.959

334.829

 

0.145

 

0.959

102.056

0.004334

Black Cherry

0.033

393.336

 

0.145

 

0.033

119.889

0.004334

White Elm

0.634

440.496

 

0.145

 

0.634

134.263

0.004334

Ironwood

1.877

332.585

 

0.145

 

1.877

101.372

0.004334

Red Oak

1.512

336.509

 

0.145

 

1.512

102.568

0.004334

 

 

References

 

Honer, T.G. 1967. Standard volume tables and merchantable conversion factors for the commercial tree species of central and eastern Canada. Can. Dept. Forestry Rural Devel., For. Mgmt. Res. and Serv. Inst. Info. Rep. FMR-X-5.

 

Honer, T.G., Ker, M.F. and Alemdag, I.S. 1983. Metric timber tables for the commercial tree species of central and eastern Canada. Maritimes For. Res. Centre. Info. Rep. M-X-140.

 

Shailer, S., Kershaw, J.A., and Zundel, P. 1998. Comparison of total volume equations for use in southwestern New Brunswick. Research Report perpared for Georgia Pacific (The Timber Company), St. Croix district.